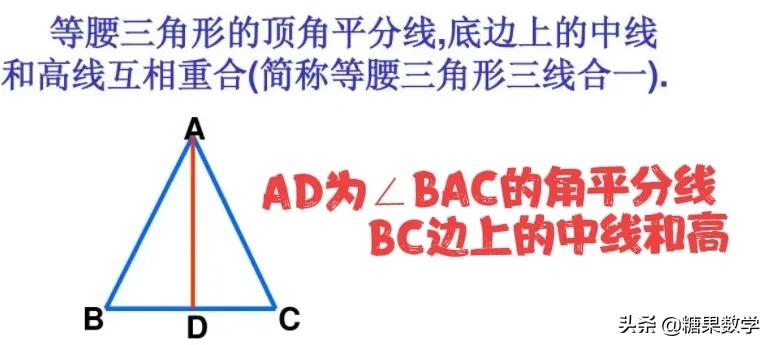
三线合一，即在等腰三角形中（前提）顶角的角平分线，底边的中线，底边的高线，三条线互相重合（前提一定是在等腰三角形中，其它三角形不适用）。

等腰三角形三线合一

同时“三线合一”又是一种判定等腰三角形的一种方法:

1、如果三角形中有一角的角平分线和它所对边的高重合，那么这个三角形是等腰三角形。

2、如果三角形中有一边的中线和这条边上的高重合，那么这个三角形是等腰三角形。

3、如果三角形中有一角的角平分线和它所对边的中线重合，那么这个三角形是等腰三角形。

三线合一证明过程:

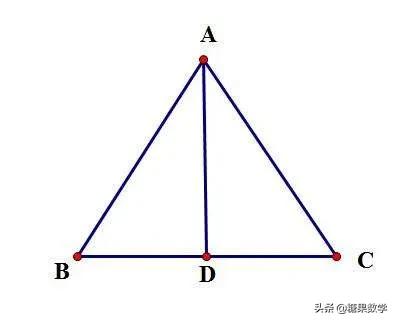
已知:如图△ABC为等腰三角形，AB=AC, AD为BC边上的中线。

求证: AD⊥BC，∠BAD=∠CAD

证明:∵ △ABC等腰三角形 AB=AC

∴∠B=∠C

在△ABD和△ACD中:

∵BD=DC

AB=AC

AD=AD

∴△ADB=ΔADC

∴∠BAD=∠CAD，∠ADB=∠ADC

∵∠ADB+∠ADC=∠BDC，且∠BDC=180度

∴∠ADB=∠ADC=90°

∴AD⊥BC